 |
 |
 |
 |
 |
Modellierung
Modell und Wirklichkeit
Mag auch lange Zeit die Physik der klassische Anwendungsbereich der Mathematik gewesen sein – so dass Galilei behaupten konnte: „Das Buch des Universums ist in mathematischen Lettern geschrieben.”
– erschließt sie sich doch immer weitere Anwendungsbereiche, je mehr wir erkennen, dass auch ehedem als unmathematisch geltende Gebiete der mathematischen Beschreibung zugänglich sind.
Die Statistik hat uns solche Betätigungsfelder eröffnet, indem sie uns ermöglichte, Chancen abzuwägen, Gefahren einzuschätzen, kurz: rationale Entscheidungen zu treffen auch im Falle fehlender Gewissheit. Es mangelt uns dabei aber immer noch jenes Gefühl, das sich in der mathematischen Physik wie von selber einstellt, dass nämlich die Formeln nicht nur die Phänomene einigermaßen korrekt wiedergeben, sondern darüber hinaus Ursachen mit Wirkungen auf einsichtige Weise verknüpfen.
Fahrzeugstau
Anders bei Versuchen, unter Inkaufnahme extremer Vereinfachungen Wirklichkeit nachzubilden – Modellierung. Ein Beispiel soll illustrieren, wie man sich so etwas vorzustellen hat.

Manchmal kommt es bei viel Verkehr „aus dem Nichts heraus” zum Stau. Es braucht keinen Unfall, keine Baustelle, kein Hindernis, es passiert „einfach so”. Wie soll man das verstehen? Jede Fahrbahn hat eine bestimmte Kapazität, ein bestimmtes Fassungsvermögen, sie lässt eine bestimmte Zahl von Fahrzeugen durch. Wovon mag diese Kapazität abhängen? Von der Geschwindigkeit der Fahrzeuge, sicherlich, und sonst noch? Vom gegenseitigen Abstand möglicherweise. Aber wie hängt das alles zusammen? Die Erfahrung – und die Vorsicht – gebietet, bei höherer Geschwindigkeit einen größeren Abstand zum Vordermann einzuhalten.Geht das auch genauer?

Erst einmal müssen wir überlegen, wie wir die Kapazität der Fahrbahn in den Griff kriegen. Eine Möglichkeit wäre, den zeitliche Abstand abzuschätzen, in dem zwei aufeinanderfolgende Fahrzeuge dieselbe Stelle passieren. Wir nehmen a als den Abstand zweier aufeinanderfolgender Fahrzeuge, v als ihre Geschwindigkeit, und t sei die gesuchte Zeitspanne. Das hintere Fahrzeug legt mit seiner Geschwindigkeit v die Strecke a in der Zeit t zurück. Dann gilt Geschwindigkeit gleich Weg durch Zeit, als Formel
| v | = | a | , |
| t |
| t | = | a | . |
| v |
Teilt man eine Stunde, hier natürlich 3600 Sekunden, durch diese Zeitspanne, so erhält man die Anzahl n der Fahrzeuge, die einen Beobachtungspunkt binnen einer Stunde passieren:
| n | = | 3600 | = | 3600 | v | . |
| t | a | |||||
Die Zwei-Sekunden-Regel
Das hilft uns nicht viel, solange wir nicht sehen, wie denn der Abstand mit der Geschwindigkeit zusammenhängt. Eine einfache Regel ist die „Zwei-Sekunden-Regel”: Wenn ich sehe, dass mein Vordermann eine bestimmte Stelle passiert, den Schatten einer Brücke zum Beispiel, soll es zwei Sekunden dauern, bis ich selbst an dieser Stelle vorbeikomme. Ich lege also den Abstand a in zwei Sekunden zurück, d. h.
Egal wie groß die Geschwindigkeit ist, in einer Stunde können immer 1800 Fahrzeuge an einem Beobachter vorbeiflitzen. Zu rechnen bleibt da nichts.
Der halbe Tachoabstand
Eine andere Regel besagt, mein Abstand zum Vordermann, gemessen in Metern, soll die Hälfte der Geschwindigkeitsanzeige, angegeben in Kilometer pro Stunde, betragen, bei 50 km/h also 25 m. Das bringt ein kleines Umrechnungsproblem mit sich, denn die Einheiten sollten schon zueinander passen. Man erreicht das aber leicht, wenn man Strecken grundsätzlich in Metern, Zeiten in Sekunden und Geschwindigkeiten in Meter pro Sekunde misst. Für die Tachometeranzeige muss man dann die Geschwindigkeit mit 3,6 multiplizieren, denn ein Meter pro Sekunde entspricht 3600 Metern in 3600 Sekunden, d. h. 3,6 km/h.
| a | = | 3,6 | v | = | 1,8 | v | , |
| 2 |
| n | = | 3600 | v | = | 2000 | . |
| 1,8 | v |
Die Zeitspanne zwischen zwei Fahrzeugen beträgt 1,8 Sekunden, in einer Stunde können 2000 Fahrzeuge passieren. Das ist kein so grundsätzlich anderes Ergebnis als zuvor. Wieder spielt die Geschwindigkeit keine Rolle.
Halber Tachoabstand plus Fahrzeuglänge

Der sichtbare Abstand ist ja eigentlich die Entfernung d zwischen der hinteren Stoßstange des Vordermanns zur vorderen Stoßstange des Hintermanns. Dann muss aber die Fahrzeuglänge l noch hinzugenommen werden. Denken wir uns, es ist Sonntag, es sind keine LKW unterwegs, sondern lauter PKW auf der Fahrt ins Blaue. Dann ist es vielleicht erlaubt, eine ziemlich einheitliche Fahrzeuglänge von etwa 5 Metern anzunehmen. Damit ergibt sich der Reihe nach
| a | = | 3,6 | v | + | 5 | = | 1,8 | v | + | 5 | , |
| 2 |
| n | = | 3600 | v | . | ||
| 1,8 | v + | 5 |
Jetzt ist n eine Funktion von v, und diese Funktion sieht folgendermaßen aus:
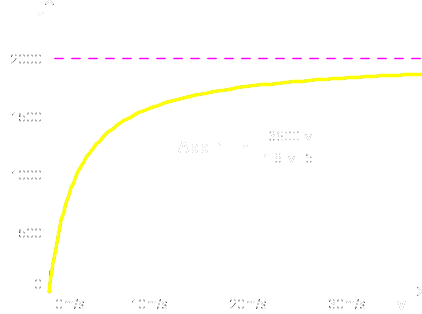
Die Anzahl n der Fahrzeuge pro Stunde nähert sich mit wachsender Geschwindigkeit v asymptotisch dem Wert 2000, den wir als Ergebnis unter Ziffer 2 schon erhalten hatten. Demnach also wäre es ratsam, möglichst schnell zu fahren, weil dann mehr Fahrzeuge durchkommen. Ganz hohe Geschwindigkeiten bringen aber nicht mehr allzu viel, weil n dort nicht mehr nennenswert zunimmt. Und gleichgültig wie schnell man auch fährt, über 2000 Fahrzeuge kommt man sowieso nicht. (30 m/s sind immerhin schon 108 km/h.)
Die Bremswegregel der Fahrschule
In der Fahrschule lernt man den Bremsweg eines Fahrzeugs nach folgender Regel abzuschätzen: Nimm die Geschwindigkeit in km/h, teile sie durch 10 und multipliziere das Ergebnis mit sich selbst, dann erhältst du den Bremsweg in Metern. Tatsächlich ist der Bremsweg unter optimalen Bedingungen – trockene Fahrbahn, griffiger Straßenbelag, tadellose Reifen – nur etwa halb so groß, aber das wollen wir im Moment noch außer Acht lassen.
In dieser Regel steckt die physikalische Erkenntnis, dass der Bremsweg nicht proportional zur Geschwindigkeit zunimmt, sondern viel stärker: Eine Verdoppelung der Geschwindigkeit hat einen viermal so langen Bremsweg zur Folge. Bei 50 km/h erhalten wir in Übereinstimmung mit dem halben Tachoabstand eine Bremsweg von 52 m = 25 m, bei 100 km/h hingegen 100 m statt der vorher errechneten 50 m.
Verzichten wir im Moment noch auf die Berücksichtigung der Fahrzeuglänge und denken wir wieder an die Umrechnung von m/s in km/h, so erhalten wir:
| a | = | ( | 3,6 | v | ) | 2 | = | 0,1296 | v 2 | , |
| 10 |
| n | = | 3600 | v | = | 3600 | . | |
| 0,1296 | v 2 | 0,1296 | v |
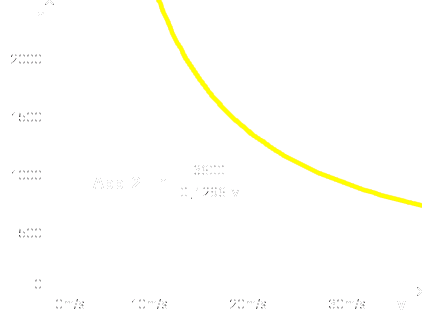
Entgegen dem vorigen Ergebnis zeigt sich hier, dass schnelles Fahren kontraproduktiv ist. Die Zahl der Fahrzeuge sinkt mit zunehmender Geschwindigkeit. Der Grund ist, dass der Bremsweg mit zunehmender Geschwindigkeit überproportionel wächst. Das sollte einen schon nachdenklich machen.
Bremsweg plus Fahrzeuglänge
Eigenartig erscheint im letzten Diagramm, dass für ganz geringe Geschwindigkeiten die Anzahl der Fahrzeuge so maßlos zunimmt. Aber wir haben ja auch außer Acht gelassen, dass dem Bremsweg die Fahrzeuglänge hinzuzufügen ist. Wir belassen es beim Zahlenwert 5 m für die Fahrzeuglänge.
| a | = | ( | 3,6 | v | ) | 2 | + | 5 | = | 0,1296 | v 2 | + | 5 | , |
| 10 |
| n | = | 3600 | v | . | ||
| 0,1296 | v 2 | + | 5 |
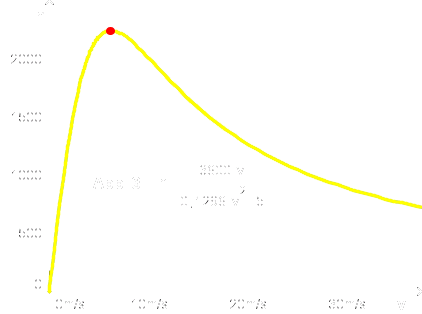
Hier ergibt sich nun ein völlig neuartiges Bild, sozusagen eine Kombination der Abbildungen 1 und 2. Für ganz kleine und ganz große Geschwindigkeiten ist die die Fahrzeugzahl gering. Dazwischen liegt irgendwo ein recht hoher Wert. Dieses Maximum liegt bei der recht niedrigen Geschwindigkeit 6,21 m/s = 22,4 km/h. Die Fahrzeugzahl beträgt dann 2236 Fahrzeuge pro Stunde. Bei 20 m/s = 72 km/h sind es nur noch gut die Hälfte, nämlich 1266 Fahrzeuge pro Stunde.
Hier zeigt uns die mathematische Analyse eine Möglichkeit auf, einen recht komplexen Vorgang zu verstehen, den sogenannten „zähfließenden Verkehr”. Er beruht eben nicht darauf, dass sich irgendwelche Verkehrsteilnehmer ungeschickt anstellen und den ganzen Verkehr aufhalten. Er stellt sich vielmehr ein, wenn alle sich regelkonform verhalten und den vorgeschriebenen Abstand einhalten. Ein Abweichen von der ermittelten Idealgeschwindigkeit würde den Verkehrsfluss weiter reduzieren.
Der Reaktionsweg
Der Bremsweg ist die Strecke, die das Fahrzeug zurücklegt, während es bremst. Aber bis es dazu kommt, muss der Fahrer erst einmal die Bremse betätigen. Zwischen dem Erkennen einer Gefahrensituation und dem Ansprechen der Bremse vergeht eine gewisse Zeitspanne, die Reaktionszeit. Diese beträgt individuell unterschiedlich eine halbe bis eine ganze Sekunde, bei entspannter Fahrweise, wenn man mit nichts Bösem rechnet, eher eine ganze Sekunde. Während dieser Zeit fährt das Fahrzeug ungebremst weiter und legt noch eine erhebliche Strecke zurück, den Reaktionsweg.
Bei einer angenommenen Reaktionszeit von einer Sekunde bewegt sich das Auto mit der Geschwindigkeit v weiter und legt dabei die Strecke r = v · 1 = v zurück. Außer der Fahrzeuglänge ist auch dieser Reaktionsweg dem Bremsweg hinzuzurechnen.
| a | = | ( | 3,6 | v | ) | 2 | + | v | + | 5 | = | 0,1296 | v 2 | + | v | + | 5 | , |
| 10 |
| n | = | 3600 | v | . | ||||
| 0,1296 | v 2 | + | v | + | 5 |
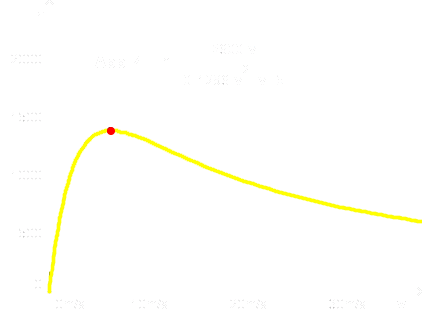
Grundsätzlich Neues passiert da nicht. Im großen und ganzen verläuft die Funktion wie ohne diese Verfeinerung. Wir haben ein Maximum bei derselben Geschwindigkeit 6,21 m/s = 22,4 km/h. Unterschied: es ist nur noch gut halb so hoch wie zuvor, nämlich 1379 Fahrzeuge pro Stunde.
Offenbar haben wir hier einen grundlegenden und wichtigen Zusammenhang entdeckt: Den größten Durchsatz an Fahrzeugen erzielt man dann, wenn alle die gleiche niedrige Geschwindigkeit von ca. 20 km/h einhalten.
Variationen
Wie schon in Ziffer 4 angedeutet, kann unter guten Bedinungen der Bremsweg durchaus kürzer sein als mit der Fahrschulregel ermittelt. Aber wenn der Bremsweg nur 80 oder 60 Prozent davon beträgt, kann ich die Rechnung mit einer kleinen Abwandlung immer noch so durchführen. Das Ergebnis sehen wir in Diagramm 5: Das Maximum der Funktion verschiebt sich geringfügig zu einer höheren Geschwindigkeit, und es fällt auch etwas größer aus, aber die eben getroffene Aussage bleibt trotzdem grundsätzlich richtig.
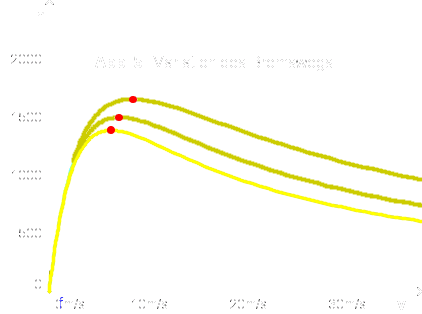
Wir haben unsere Rechnungen unter sehr starken Vereinfachungen angesetzt. Insbesondere haben wir unterstellt, dass alle Fahrer sich gewissenhaft, zumindest im Mittel, an die errechneten Abstände halten. Aber auch wenn sie nur 80 oder 20 Prozent dieses Abstandes einhalten, ergibt sich kein anderes Bild. Der Fahrzeugdurchsatz wird höher, aber die Geschwindigkeit, bei der man das Maximum an Durchsatz erzielt, ändert sich nicht
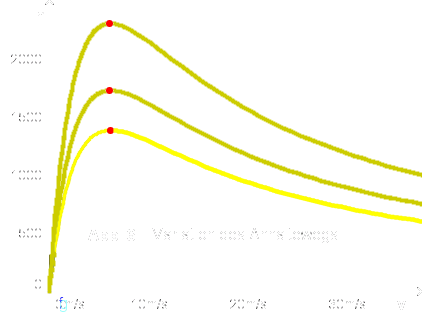
Ungelöst bleiben allerdings zwei Probleme:
- Welchen Einfluss auf das Ergebnis hat es, wenn die Fahrer ihre Abstände sehr individuell und stark voneinander abweichend wählen?
- Welchen Einfluss auf das Ergebnis hat es, wenn die Fahrer nicht einmal annähernd ihren Abstand in Einklang mit den obigen Formeln wählen?
Hier würden möglicherweise statistische Methoden ein Stück weiterhelfen. Und natürlich bedürfen die Ergebnisse einer empirischen Überprüfung. Sie klingen plausibel und stehen im Einklang mit Erfahrungen, die jeder schon einmal gemacht hat. Sie geben auch für gewisse Erscheinungen nachvollziehbare Ursachen an. Und sie können vielleicht theoretische Grundlagen für Fahrer-Assistenzsysteme wie Tempomat oder Abstandswarner liefern. Aber der Knackpunkt bleibt: Liefern sie ein angemessenes und stimmiges Bild der Wirklichkeit?