Bruchrechnung

Wozu Bruchzahlen?

Niemand mehr rechnet heute mit 3/8 Pfund Kaffee oder 1/5 Euro. Die Dezimalbrüche sind ja so viel bequemer, und im Zeitalter elektronischer Rechenhilfen erst recht. Warum also immer noch diese Quälerei mit den Brüchen, zumal heute Taschenrechner auch die Bruchrechnung beherrschen?

Der Grund liegt im Umgang mit algebraischen Ausdrücken. Auch das beherrschen heute viele Computerprogramme und einige Taschenrechner aus dem EffEff, wenn sie nämlich über ein Computer-Algebra-System, kurz CAS, verfügen. Die leistungsfähigsten darunter können sogar Gleichungen lösen, differenzieren, integrieren, Grenzwerte berechnen, mit Vektoren und Gleichungssystemen umgehen.

Aber das Gefühl, diesen Maschinchen ausgeliefert zu sein, schafft doch ein wenig Unbehagen. Man hat sie möglicherweise auch nicht immer und überall zur Hand. Und vielleicht möchte man doch verstehen, was eigentlich dahinter steckt.

Bruchzahlen sind aus Teilungsproblemen entstanden. 120 Rinder auf 5 Söhne aufzuteilen, ist so ein Teilungsproblem. Dieses macht uns allerdings keine Mühe, 120 : 5 = 24, d.h. jeder Sohn erhält 24 Rinder. Bei 123 Rindern bleiben 3 Rinder übrig, am besten opfert man sie den Göttern.

2 Scheffel Getreide unter 8 Knechten zu verteilen, ist eine Aufgabe von ganz anderem Kaliber. Den unteilbaren Rest den Göttern zu opfern, würde bedeuten, dass alle 8 Knechte leer ausgehen. Das wäre schlecht. Angemessener ist es, jedem den vierten Teil eines Scheffels zukommen zu lassen. Schon haben wir einen Bruch:

Solche logistischen Probleme waren bereits im alten Ägypten zu lösen. Waren doch die zum Bau der riesigen Tempelanlagen und Pyramiden abkommandierten Menschenmassen zu versorgen. Kein Wunder, dass man bereits eine auf diese praktischen Probleme zugeschnittene Bruchrechnung beherrschte. Der Unterhalt großer Heere machte zu allen Zeiten den Umgang mit solchen Überlegungen erforderlich.

Gleichheit von Brüchen

Ein Viertel ist ursprünglich ein Viert-Teil, der vierte Teil von einem Ganzen, einem Scheffel Weizen, einem Fuder Heu, einer Pizza. Nun kann man, wenn viele Leutezu verköstigen sind, das Viertel einer Riesen-Pizza weiter unterteilen.

Teilt man das Viertel, jedes Viertel, noch einmal in drei Teile, so erhält man 12 Pizzastücke, also Zwölftel, und das Viertel besteht aus drei solchen Zwölfteln. Formal gesehen hat man nichts weiter getan als den Zähler und den Nenner von 1/4 mit 3 zu multiplizieren. Man nennt diesen Vorgang Erweitern. Erweitern heißt, Zähler und Nenner mit derselben Zahl zu multiplizieren. Erweitern ändert den Wert eines Bruches nicht.

Das funktioniert auch mit algebraischen Ausdrücken.

Auch umgekehrt wird ein Schuh draus. Teilt man Zähler und Nenner durch dieselbe Zahl, so es denn geht, ändert sich der Wert des Bruches ebensowenig. Diesen Vorgang nennt man Kürzen.

Addition und Subtraktion

Und jetzt zum Rechnen. Um zu 3/4 noch 1/4 hinzu zu fügen oder davon 1/4 weg zu nehmen, bedarf es keiner besonderen geistigen Verrenkungen.

So einfach ist das immer, wenn zwei Brüche denselben Nenner haben, gleichnamig sind. Dann sind nur die Zähler zu addieren bzw. zu subtrahieren. (Manche werfen das mit der später dargelegten Multiplikation durcheinander und addieren bzw. subtrahieren die Nenner ebenfalls. So ein Unsinn!) Andere Brüche muss man durch geeignetes Erweitern zuvor gleichnamig machen. Nehmen wir die Brüche 3/4 und 2/5 und bilden wir die Differenz.

Weiter auf dieselbe Weise.

Das letzte Beispiel zeigt uns, dass, wenn dem Ganzen auch einfache Regeln zu Grunde liegen, die Umsetzungen durchaus anspruchsvoll sein können.

Multiplikation

Wir erinnern uns, dass man die Fläche eines Rechtecks als Länge mal Breite bestimmt. Nehmen wir als Beispiel das Produkt 4 · 6.

Genauso wollen wir es halten, wenn Länge und Breite Brüche sind, im Beispiel 3/4 und 2/5. Wir teilen diem eine Seite des 1m-Quadrates in 4 Teile, von denen wir 3 herausgreifen. Die andere Seite teilen wir in 5 Teile, von denen wir 2 herausgreifen. Damit haben wir da 1m-Quadrat in 20 Teile aufgeteilt, und 20 ist gerade das Produkt der Nenner 4 · 5. Das gesuchte Produkt umfasst davon 6 Teile., und 6 ist das Produkt der Zähler 3 · 2.

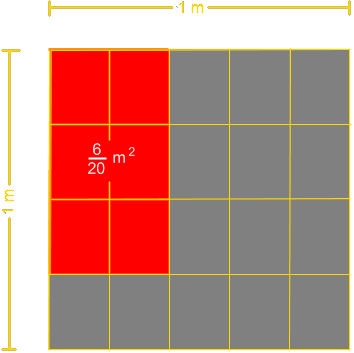
So kommen wir zur Regel für die Bruchmultiplikation: Zähler mal Zähler und Nenner mal Nenner. Es spart Mühe, wenn man so früh wie möglich ans Kürzen denkt.

Das letzte Beispiel führt uns auf ein weiteres allgemeines Prinzip: Multipliziert man einen Bruch mit seinem Kehrwert, ist das Ergebnis 1. (Man erhält den Kehrwert, indem man Zähler und Nenner vertauscht.) Das wird uns im Folgenden helfen.

Division

Wir haben soeben beobachtet, dass das Produkt aus einem Bruch und seinem Kehrwert stets 1 ergibt. Ebenfalls ergibt es 1, wenn man eine Zahl, auch eine Bruchzahl, durch sich selber teilt.

Das gibt Anlass zu der Vermutung, dass die Division durch einen Bruch und die Multiplikation mit seinem Kehrwert dasselbe bewirken. Das ist tatsächlich zutreffend, wie der folgende kleine Beweis zeigt. Dabei sollen a und b zwei Zahlen sein, b auf jeden Fall eine Bruchzahl und b' der Kehrwert von b.

Dividiert man zwei Brüche durch einander, so nimmt man von dem zweiten (und nur von dem zweiten!) den Kehrwert und multipliziert.