Imaginäre Zahlen

„[…]

Auf einmal kreischt ein Neid durch die Volière;

sie aber haben sich erstaunt gestreckt

und schreiten einzeln ins Imaginäre.”

(Rainer Maria Rilke, Die Flamingos)

Zahlenstrahl

Der Zahlenstrahl als bildliche Darstellung der Zahlen ist uns allen vertraut. Er leistet aber viel mehr, als nur die Lage der Zahlen zueinander zu verdeutlichen. Auch das Rechnen mit den Zahlen kann er uns veranschaulichen.

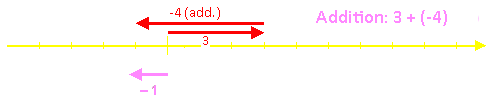
Stellt man Zahlen als Pfeile mit der entsprechenden Länge dar, ist die Addition nichts weiter als das Aneinanderhängen der Pfeile.

Eine negative Zahl erhält man, indem man den entsprechenden Pfeil in die Gegenrichtung klappt.

Die Subtraktion ist das Gegenteil der Addition, also lässt man den zu subtrahierenden Pfeil entgegen seiner ursprünglichen Richtung laufen. Da zeigt sich, dass die Subtraktion einer Zahl mit der Addition ihrer Gegenzahl identisch ist.

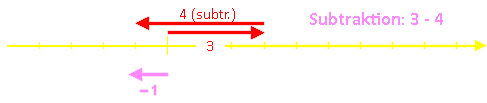
Entsprechend verfährt man bei der Subtraktion einer negativen Zahl, man trägt auch sie entgegen ihrer ursprünglichen Richtung ab.

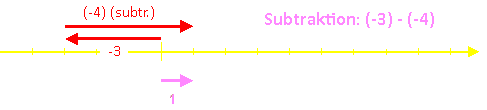
Multiplikation mit −1

Das Vervielfachen geschieht auf naheliegende Weise. Es soll hier nicht weiter verfolgt werden. Wichtiger ist, dass wir uns noch einmal deutlich machen, wie man zu einer Zahl die Gegenzahl erhält: rechnerisch multipliziert man mit −1, am Zahlenstrahl klappt man den Pfeil in die Gegenrichtung. Man kann das auch als eine Drehung um 180^o ansehen. Eine weitere Drehung um 180^o bzw. eine weitere Multiplikation mit −1 stellt den Ausgangszustand wieder her. Wir erinnern uns dabei an die Regel „minus mal minus ergibt plus”.

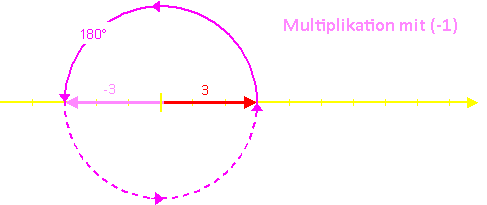
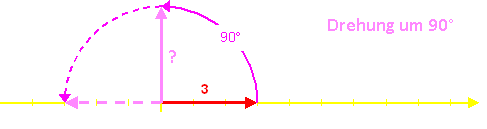
Noch einmal zum Festhalten: Das Multiplizieren mit −1 entspricht einer Drehung um 180^o, mehrfaches Multiplizieren mit −1 erfordert, dass mehrere Drehungen nacheinander ausgeführt werden. Man kann aber auch um weniger als 180^o drehen, beispielsweise nur um 90^o. Das sieht dann so aus:

Die Zahlenebene

Dabei verlässt der Ergebnispfeil allerdings den vertrauten Zahlenstrahl und weist irgendwo ins Nirgendwo. Zwei solche Drehungen, hintereinander ausgeführt, entsprechen einer Multiplikation mit −1. Interpretieren wir die Drehung um 90^o als eine Multiplikation mit dem Faktor i, so entsprechen beide Drehungen zusammen einer wiederholten Multiplikation mit dem Faktor i. Zweimaliges Multiplizieren mit i entspricht einer Multiplikation mit −1.

Dazu muss man allerdings den Zahlenstrahl ergänzen um weitere Objekte, die neben demselben liegen. Damit wir nicht dauernd neue Bezeichnungen erfinden müssen, behalten wir auch für diese Objekte die Bezeichnung „Zahlen” bei, verstehen aber diese Bezeichnung hinfort in einem erweiterten Sinn. Wir erweitern damit den – eindimensionalen – Zahlenstrahl zu einer – zweidimensionalen – Zahlenebene. In dieser sind nun noch weit mehr Pfeile unterzubringen als nur waagerecht oder senkrecht verlaufende.

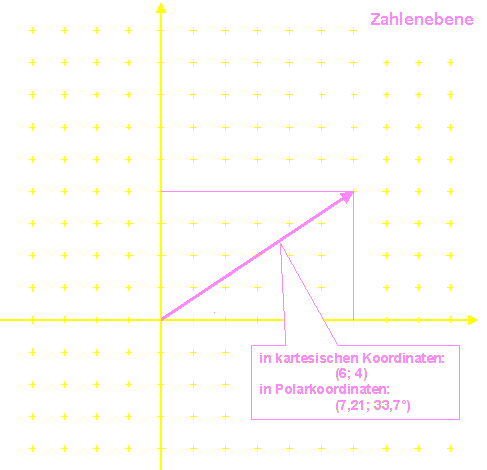
Wir müssen zu dem vertrauten Zahlenstrahl einen weiteren, und zwar einen nach oben weisenden Strahl hinzunehmen. Am besten geben wir ihm auch gleich einen Namen, „Erweiterungszahlen” wäre ein durchaus passender Vorschlag. Aus historischen Gründen hat sich der unsägliche Name „imaginäre Achse” eingebürgert, als handle es sich dabei um mathematische Spintisiererei (die altvertrauten Zahlen bilden die „reelle Achse”). Was tatsächlich befremdlich wirken mag, ist die eigenartige Eigenschaft des oben genannten Faktors i, quadriert −1 zu ergeben. Das ist eine ganz neuartige Erfahrung, weil es bei den Zahlen auf dem ursprünglichen Zahlenstrahl so etwas nicht gibt. Aber schließlich sind wir ja mit diesen Zahlen vom ursprünglichen Zahlenstrahl abgewichen.

Die Gesamtheit der damit verfügbaren Zahlen bezeichnet man als die „komplexen Zahlen”. Als nächstes müssten wir nun in Erfahrung bringen, wie man mit diesen Zahlen zu rechnen hat. Dabei soll aber alles, was wir über die vertrauten Zahlen wissen, gültig bleiben. Wen es wirklich interessiert, sollte in einem Lehrbuch oder bei WIKIPEDIA nachschlagen. Wir können uns das hier ersparen.

Bleibt noch die Fragen nach dem Sinn und Zweck dieser komplexen Zahlen. Oder sind sie am Ende doch nichts weiter als eine geistreiche mathematische Freizeitbeschäftigung?

Eine Anwendung

Eine Bewegung wie nebenstehend dargestellt nennt man eine Schwingung. Charakteristisch dafür ist die recht große Geschwindigkeit in der Mitte und eine Abnahme der Geschwindigkeit zu den Enden hin, wobei der Körper in den Endpunkten kurz zu verharren scheint. Solche Schwingungen spielen in der Physik an vielen Stellen eine entscheidende Rolle. Federn schwingen, Pendel schwingen, Luftmoleküle schwingen – man nennt das „Töne” –, elektrische Schwingkreise schwingen, hier allerdings ändert sich nicht der Ort periodisch, sondern die Spannung, genauso wie beim Schwingen des Wechselstroms. Wellenbewegungen beruhen auf Schwingungen, damit auch die Fülle der elektromagnetischen Wellen, von den Funk- und Radarwellen über die Wellen des sichtbaren Lichtes bis hin zu den Röntgen- und Gammastrahlen. Und selbst Elektronen besitzen neben ihren Teilchen- auch Welleneigenschaften.

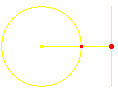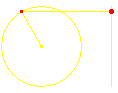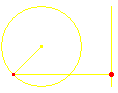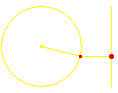
Der Ablauf einer solchen Schwingungsbewegung wird durchsichtiger, wenn man sich dazu eine Kreisbewegung vorstellt, welche durch Projektion diese Schwingung hervorruft. Und eine Kreisbewegung ist mathematisch besonders einfach zu handhaben, wenn man sie mithilfe der komplexen Zahlen beschreibt. Da also geht es mit den komplexen Zahlen leichter als ohne sie. Das ist übrigens an manchen Stellen in der Mathematik so, dass das vermeintlich größere und umfassendere Problem leichter zu lösen ist. Ein anderes Beispiel für diese Erfahrung ist der Beweis des Eulerschen Polyedersatzes; er wird für alle nach bestimmten Regeln aufzubauenden Gebilde geführt, von denen die Polyeder nur Sonderfälle sind.