 |
 |
 |
 |
 |
Chancen und Risiken
Zählen und Messen
Es kommt uns selbstverständlich vor, dass man Dinge, Objekte zählt, obwohl dahinter doch schon die immense Verstandesleistung steckt, diese Dinge einerseits als so gleichartig anzusehen, dass sie zum Zählen zusammengefasst und von der schier unerschöpflichen Fülle aller anderen Objekte abgegrenzt werden können, sie andererseits aber so sauber voneinander zu unterscheiden, dass sie jedes für sich als Individuum wahrgenommen werden können. Wie weit war dann noch der Weg, vom Zählen zum Messen fortzuschreiten, was uns die Brüche und die Dezimalzahlen bescherte.
Aber auch wenn wir messen, haben wir es zunächst immer noch mit konkreten Eigenschaften von konkreten Dingen zu tun, mit der Länge eines Schiffes, der Fläche eines Ackers, dem Gewicht eines Kupferbarrens. Im Laufe der Zeit entdeckt man immer weitere Messgrößen, die Zeit, die Temperatur, die elektrische Ladung, den pH-Wert einer Säure, schließlich sogar abstrakte Größen wie Beschleunigung, Drehmoment, Arbeit.
Es bleibt immer noch ein Riesenschritt, auch Chancen und Risiken durch Zahlen auszudrücken. Hier ist kein Messen mehr im Spiel, aber was dann? Dinge – werden gezählt, ihre Eigenschaften – gemessen. Andere Messgrößen lassen sich durch nachvollziehbare Formeln daraus berechnen. Aber Chancen und Risiken? Die Chance, eine Eintrittskarte für das gewünschte Fußballspiel zu erhalten, das Risiko, eine bestimmte Krankheit zu bekommen – – . Abstrakt gesprochen haben wir es hier nicht mit einer Eigenschaft von Dingen zu tun, die gemessen wird, sondern mit einer Eigenschaft von Situationen oder Ereignissen, der man einen Zahlenwert zuordnet. Damit das Kind einen Namen hat, nennt man diese Eigenschaft von Ereignissen ihre Wahrscheinlichkeit.
Wahrscheinlichkeit
Wahrscheinlichkeit ist keine physikalische Eigenschaft oder Messgröße. Insofern hat sie auch keine physikalische Dimension, und es gibt keine Einheit für diese Größe. Man muss sie anders festsetzen. Welcher Mannschaft bei einem Fußballspiel der Anstoß zukommt, entscheidet der Schiedsrichter per Münzwurf. Das empfinden wir als „fair”, beide Mannschaften haben dieselbe Chance, wir beschreiben diese als „fifty-fifty” oder „halbe-halbe”. Wir wissen hundertprozentig, eine der Mannschaften wird den Anstoß bekommen. Wenn beide Mannschaften dieselbe Chance haben, macht das für jede fünfzig Prozent. Diese Überlegung liegt der Festsetzung eines Zahlenwertes für die Wahrscheinlichkeit zugrunde. Zum leichteren Rechnen schreiben wir sie in der Form 50 % = 50 / 100 = 0,5.
Wahrscheinlichkeit wird nicht gemessen, sondern vermutet. Dass man trotzdem mit Wahrscheinlichkeiten rechnen, Mathematik treiben kann und zu aussagekräftigen Schlussfolgerungen kommt, scheint der glasklaren Schärfe der Mathematik zu widersprechen. Wenn – Vermutung – 50% der Bevölkerung männlichen Geschlechtes sind, und wenn – Vermutung – 8% aller männlichen und 1% aller weiblichen Personen unter Rot-Grün-Blindheit leiden, dann sind – Schlussfolgerung – 4,5 Prozent von allen Personen rot-grün-blind.
Das ist nun nicht einfach nur der Mittelwert. Es sieht nur so aus, weil sich Männlich und Weiblich nach unsrer Annahme halbe-halbe verteilen. Korrekt erhält man das Ergebnis mittels eines Wahrscheinlichkeitsbaumes.
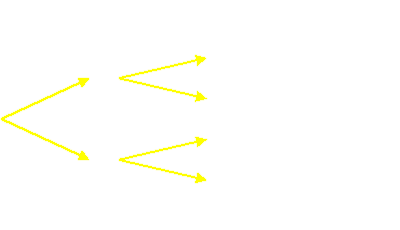
Im ersten Schritt befassen wir uns mit dem Geschlecht, wir setzen 50% männliche und 50% weibliche Personen voraus. Im zweiten Schritt notieren wir für beide Geschlechter die angenommenen Wahrscheinlichkeiten, mit oder ohne diesen Defekt zu leben. Weitere Schritte könnten sich anschließen, in unserem Beispiel sind wir mit zweien fertig. Wenn 50% männlich sind und von diesen wiederum 8% rot-grün-blind, führt das auf einen Anteil von 4% farbenblinder Männer in der Gesamtbevölkerung. Das erhält man durch die Multiplikation 50% · 8% = 0,5 · 0,08 = 0,04 = 4%. Fehlen noch die Frauen. Zum Schluß muss man noch die farbenblinden Männer und Frauen addieren und – voilá.
Die Vorgehensweise folgt diesem Schema:
- Teile die Stufen ab.
- Notiere die einzelnen Wahrscheinlichkeiten. Dabei müssen die Wahrscheinlichkeiten derjenigen Pfeile, die von ein und demselben Punkt ausgehen, sich zu 1 ergänzen.
- Berechne die Wahrscheinlichkeiten längs der verschiedenen Pfeilketten, der sogenannten „Pfade” im Wahrscheinlichkeitsbaum; multipliziere dazu die Einzelwahrscheinlichkeiten.
- Die Summe aller Pfadwahrscheinlichkeiten muss wiederum 1 ergeben.
- Sondere die interessierenden Pfade aus und addiere ihre Pfadwahrscheinlichkeiten.
Bleibt man bei den oben gesetzten Vermutungen, so hat ein Ungeborenes die Wahrscheinlichkeit 4,5%, mit Rot-Grün-Blindheit zur Welt zu kommen. Ist allerdings sein Geschlecht schon bekannt, so ändert sich dieser Wert je nachdem auf 8% oder 1%. Das ist die nächste Überraschung bei der Wahrscheinlichkeit, dass sie nicht ein für allemal feststeht, sondern je nach Kenntnisstand ihren Zahlenwert ändert, selbst wenn man an den Ausgangswerten festhält. Ist das ein Wunder? Vermutungen werden überdacht, wenn man sich neue Informationen verschafft.
Medizinischer Test
Von einem medizinischen Test erwartet man eigentlich absolute Zuverlässigkeit, aber dem ist nicht so. Um ein Beispiel durchzurechnen, machen wir einige Annahmen: Mit der Krankheit A seien erfahrungsgemäß 2% der Bevölkerung infiziert, man nennt das die Durchseuchung. Der für diese Krankheit entwickelte Test B werde bei 10% der Infizierten (irrtümlich) negativ, d. h. die Sensitivität betrage 90% oder 0,9. Bei 1% der Nicht-Infizierten werde er (irrtümlich) positiv,, d. h. die Spezifität betrage 99% oder 0,99. Mit welcher Wahrscheinlichkeit ist man infiziert, wenn bei einem selbst der Test positiv ausfällt? Mit welcher Wahrscheinlichkeit ist man nicht infiziert, wenn bei einem selbst der Test negativ ausfällt? Aufgepasst: Mann nennt das Ergebnis positiv, wenn die Frage „Ist der Betreffende infiziert?” bejaht wird.
Wir erstellen wieder einen Baum. 1. Stufe: infiziert? – 2. Stufe: Test positiv? Zur Verdeutlichung sind die gegebenen Zahlenwerte weiß, die daraus errechneten farbig eingetragen.
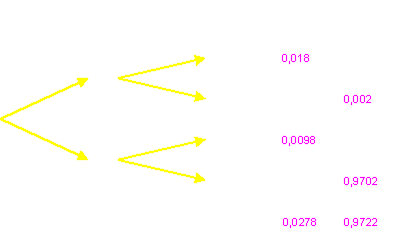
Die errechneten Zahlen haben alle ihre Bedeutung: von allen getesteten Persoenen sind 1,8 % sowohl tatsächlich infiziert als auch positiv getestet. Insgesamt wird der Test bei 2,78 % aller Personen positiv. Diese Diskrepanz bedeutet aber auch, dass der Test für knapp 1 %, genauer für 0,98 %, falschen Alarm gibt. Das ist zunächst einmal interessant, aber ist es auch wichtig?
Dieser Baum ist nur die Vorbereitung. Um herauszubekommen, welcher Anteil der positiv getesteten Personen wirklich infiziert ist bzw. welcher Anteil der negativ getesteten Personen wirklich nicht infiziert ist, muss in einem neuen Baum das Testergebnis als erste Stufe gewählt werden. Hier werden nun als bekannte Werte Ergebnisse aus dem ersten Baum verwendet, denn Pfade, die über dieselben Teilergebnisse laufen, müssen dieselbe Pfadwahrscheinlichkeit erhalten. Mit diesen gelingt es, die Teilwahrscheinlichkeiten zu bestimmen, da man ja diese Pfadwahrscheinlichkeitn durch Multiplizieren bekommt.
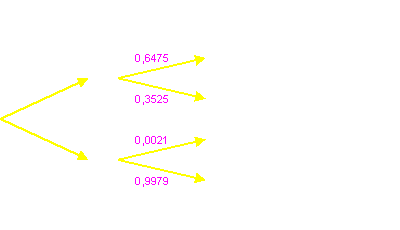
Unter den oben angegebenen Ausgangsbedingungen erhält man also die Ergebnisse:
Ist das Testergebnis positiv, so ist man mit der Wahrscheinlichkeit zwei Drittel wirklich infiziert, aber mit der Wahrscheinlichkeit ein Drittel nicht infiziert. Bei negativem Testergebnis ist die Wahrscheinlichkeit, doch infiziert zu sein, etwa zwei Promille.
Das alles ist eine Folge davon, dass man bei jedem solchen Test mit Fehlern rechnen muss. Die Personen, die tatsächlich infiziert sind, sind eben nicht hundertprozentig identisch mit denjenigen, die ein positives Testergebnis hervorrufen.
Erschwerend kommt hinzu, dass auch der Anteil der Infizierten unter den positiv Getesteten ein anderer ist als der Anteil der positiv Getesteten unter den Infizierten. Das wird leicht durcheinander geworfen.

Ein Beispiel mag den Unterschied illustrieren: Im Jahre 2006 sind in Niedersachsen 1338 Personen aus EU-Ländern eingebürgert worden. Von diesen waren zum Zeitpunkt der Einbürgerung 383 Personen ledig. Den größten Anteil unter diesen Einbürgerungen hatten polnische Staatsbürger mit 864 Personen, von denen wiederum 222 ledig waren. Der Anteil der Ledigen unter den Polen betrug
| 222 | = | 25,7% | , |
| 864 |
der Anteil der Polen unter den Ledigen betrug dagegen
| 222 | = | 58,0% | . |
| 383 |
Die obigen Ergebnisse zum medizinischen Test hängen sehr stark von den Ausgangswerten ab, andere Werte können zu völlig anderen Ergebnissen führen, wie man durch Eingabe in das nachfolgende Rechenschema nachprüfen kann. (Alle Eingaben müssen Werte zwischen 0.0001 und 1 sein. Dezimalzeichen ist der Punkt, das verlangt JAVASCRIPT.)