 |
 |
 |
 |
 |
Mathematik und Logik
Erfahrungen und Schlussfolgerungen
Welche Schlüsse sind logische Schlüsse und wahr aus sich selbst heraus? Welche beruhen auf Erfahrung und stellen allenfalls anfechtbare Verallgemeinerungen dar?
Erfahrungen zu machen und zu verallgemeinern ist Gewähr unserer Lernfähigkeit, deshalb nicht geringzuschätzen. Es gibt vielerlei solche Erfahrungen:
- Beobachtungen: „Bei Nacht sind alle Katzen grau.”
- Lebensweisheiten: „Wenn zwei sich streiten, freut sich der Dritte.”
- Verallgemeinerungen: „Abendrot - Gut-Wetter-Bot′.”
- Gemeinplätze: „Nobody is perfect.”
- Sottisen: „Freunde in der Not geh′n tausend auf ein Lot.”
- Vermutungen: „Wer schläft, sündigt nicht.”
- Hoffnungen: „Ehrlich währt am längsten.”
- Vorurteile: „Was Hänschen nicht lernt, lernt Hans nimmermehr.”
- Ängste: „Wer sich in Gefahr begibt, kommt darin um.”
- Wunschvorstellungen: „Morgenstund′ hat Gold im Mund.”
- fixe Ideen: „Was bitter ist für den Mund, ist für′s Herz gesund.”
Von logischen Schlussfolgerungen verlangen wir allerdings ein noch höheres Maß an Zuverlässigkeit, eine Zuverlässigkeit, die über alle Erfahrung hinaus Zustimmung erzwingt, auch und gerade dort, wo die zugrunde liegende Erfahrung nicht geteilt wird. Trotzdem sind wir keineswegs sicher, welche logischen Schlüsse ein so hohes Maß an Zuverlässigkeit besitzen. Sätze wie „Sind zwei Größen einer dritten gleich, so sind sie untereinander gleich” erscheinen uns so selbstverständlich, dass wir ihre Anwendung jederzeit akzeptieren. Doch schon dass man sie wert findet, in dieser Form festgehalten zu werden, belegt eine gewisse Unsicherheit. Wir einigen uns darüber, auf dieser Basis zu argumentieren, und stimmen den Schlüssen mit dem Vorbehalt zu, dass der genannte Satz, mag er auch auf Erfahrung beruhen, als Axiom akzeptiert wird.
Tatsächlich formuliert Euklid1 besagten Zusammenhang als Axiom - in seinem Verständnis zwar selbstevident, nichtsdestoweniger im wörtlichen Sinne „bemerkenswert”. Er hat noch mehrere dergleichen. Für mich heißt das: „Es ist zwar völlig klar, dass es so ist, aber für alle Fälle will ich es doch lieber ausdrücklich festhalten.” Euklid war eben sehr kritisch, für ihn verstand sich nichts von selber. Oder besser: auch was sich für ihn von selber verstand, hat er ausdrücklich formuliert und seinen Schlussfolgerungen vorangestellt als gemeinsame, verbindliche Argumentationsbasis.
In unserer heutigen mathematischen Systematik betrachten wir Gleichheit als eine Äquivalenzrelation. Eine Relation R ist nur dann eine Äquivalenzrelation, wenn sie ganz bestimmte Eigenschaften besitzt. Sie hat unter anderem transitiv zu sein, d. h. folgende Bedingung zu erfüllen:
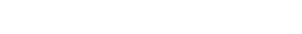
Das ist das Axiom des Euklid in moderner Schreibweise.
Syllogismen
Abgesehen davon, was sind das denn eigentlich: „Größen”? Und was bedeutet: „gleich”? Größen sind keine Dinge der uns umgebenden Welt wie Nägel, Bretter, Bohrer oder Hände, sondern quantifizierbare Eigenschaften von solchen Dingen. Die Länge eines Brettes, das Gewicht eines Nagels, die Temperatur einer Hand sind solche Eigenschaften, die, ein geeignetes Vergleichsverfahren vorausgesetzt, als gleich oder ungleich erkannt werden können. Aber die Physiker wissen, ein solcher Vergleich ist immer nur mit beschränkter Genauigkeit möglich. Nehmen wir einmal an, die angestrebte Genauigkeit betrage 1 Millimeter, das ist in jeder Tischlerei vernünftig. Brett 1 ist 0,9992 Meter lang, Brett 2 ist 1,0008 Meter lang und Brett 3 genau 1,0000 Meter. Länge 1 und Länge 2 sind gleich Länge 3, die Abweichung beträgt jedesmal 0,8 Millimeter. Untereinander sind sie nicht gleich, der Unterschied beträgt 1,6 Millimeter. Das oben zitierte Axiom gilt nicht bei einer solchen „fehlertoleranten Gleichheit”.
Aber, so ist einzuwenden, wir meinen ja hundertprozentige Gleichheit, vollkommene Gleichheit, ideale Gleichheit, Gleichheit, wie sie in dieser reinen Form in der Natur wohl kaum vorkommt. Wenn jedoch die Gleichheit in der Natur keine vollständige Entsprechung findet, wenn das Axiom nichts oder nur Ungefähres aussagt über reale Eigenschaften, trifft das auf die Schlussfolgerungen genauso zu. Und trotzdem machen wir uns mit ihnen diese immense Mühe!
Offenbar ist zu einem schlüssigen Aufbau der Mathematik zweierlei notwendig, das saubere Festhalten aller Grundaussagen (Axiome) und die Angabe der korrekten Schlussverfahren. Euklid formulierte die seiner Ansicht nach notwendigen Axiome, schon vorher hatte Aristoteles 2 zulässige Schlussregeln in Form von Syllogismen katalogisiert, gedacht als ein Axiomensystem des logischen Schließens. Ein Beispiel:
Oder in der Sprache der Mengenlehre:Alle Griechen sind Menschen.Alle Menschen sind sterblich.------------------------------------Alle Griechen sind sterblich.
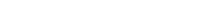

Das ist nichts anderes als die Transitivität der Teilmengenbeziehung. (Die Teilmengenbeziehung ist keine Äqivalenzrelation. Dazu fehlt ihr z. B. die Kommutativität.)
Transitivität scheint eine weit verbreitete Eigenschaft zu sein. Alle Schlussketten beruhen auf dem Prinzip der Transitivität. Aus erstens folgt zweitens, aus zweitens folgt drittens, also folgt aus erstens am Ende drittens. Von der Relation "folgt aus" zwischen Aussagen erwarten wir neben anderen Eigenschaften, dass sie transitiv ist.
Allerdings beachten wir in unserer Alltagsrede nicht unentwegt den genannten Syllogismus. Es würde uns niemals einfallen, so zu argumentieren:
Alle Griechen sind Menschen.Alle Menschen sind selbstsüchtig.----------------------------------------Alle Griechen sind selbstsüchtig.
Alle Männer sind Schweine.Alle Schweine sind niedlich.-------------------------------------Alle Männer sind niedlich.
Warum eigentlich nicht? Offenbar geht es uns im Alltag nicht immer nur um Logik, um schlüssiges Beweisen, um glasklare Wahrheiten, sondern oft um Gefühle, um Einschätzungen, um persönliche Ansichten. Nicht um Überzeugung, sondern Überredung, nicht um Erkenntnis, sondern Wirkung.
Und auch in den Wissenschaften ist Logik nur ein Weg unter vielen, der - vielleicht - zur Erkenntnis führt. Öfter noch bedient man sich anderer Wege, der Verallgemeinerung, der Analogie, der Polemik, der Pointierung, des Einfühlungsvermögens, der Provokation, der Exemplifizierung, der Vermutung, der dialektischen Überspitzung, der Kombination, der Reduktion, der Suggestion. Auch die Mathematiker bedienen sich dieser Mittel, um zu ihren Sätzen zu gelangen. Aber wenn sie dahin gelangt sind, geht die Arbeit des Beweisens los, und dabei darf man sich einzig und allein auf logische Schlüsse stützen.
Beweisen
Woher wissen wir, was logisch einwandfreie Schlüsse sind? Die Wahrheit ist: wir wissen es nicht. Nachdem Euklid seine „Elemente” zusammengestellt hatte, dauerte es nicht lange, bis die ersten Lücken in seiner Beweisführung entdeckt wurden. Dieses Wechselspiel von Beweis und Beweiskritik durchzieht die Entwicklung der Mathematik von den frühen Anfängen bis in die Gegenwart.
Im Zusammenhang mit mathematischer Schönheit habe ich als Beispiel den Beweis des Eulerschen Polyedersatzes angeführt. Ich hoffe doch, dass er dort einsichtig und logisch erscheint. Trotzdem ist der sukzessive Aufbau der Polyedernetze alles andere als unproblematisch. Nachdem man solche Beweise lange Zeit unter Rückgriff auf eine „intuitive” Logik geführt hatte, erkannte Peano2 die Notwendigkeit, diese Vorgehensweise explizit zu rechtfertigen. Dazu formulierte er seine Axiome für die natürlichen Zahlen. Das fünfte Axiom lautet sinngemäß:
Wenn 0 eine Eigenschaft E besitzt und wenn sich die Eigenschaft E von jeder Zahl auf ihren Nachfolger überträgt, dann besitzen alle natürlichen Zahlen die Eigenschaft E.
Es ist die Grundlage für das Beweisverfahren der vollständigen Induktion. (Für die Polydernetze ist damit noch nichts gewonnen, diesen Bereich decken die Peano-Axiome nicht ab. Schließlich hat ja in der Menge der Polyedernetze nicht jedes Netz einen eindeutig bestimmten Nachfolger.)
Wir benötigen also, wenn wir Mathematik treiben wollen, für jeden Teilbereich entsprechende Axiome, für die Geometrie wie für die natürlichen Zahlen, für die Topologie wie für die Analysis und für viele weitere Spezialgebiete. Darüber hinaus ein Axiomensystem der Logik, d. h. eine Auflistung der zulässigen Schlussregeln. Weil diese Axiome nicht mehr als gottgegeben oder als der Wirklichkeit immanent angesehen werden, ist es erlaubt, mit ihnen zu spielen und Alternativen auszuprobieren.
Indirekter Beweis
Wenn man alle anderen Faktoren ausschließt, muss was übrig bleibt die Wahrheit sein.(Arthur Conan Doyle, Das Zeichen der Vier)2
Euklid legten seinen „Elementen” fünf geometrische Axiome zugrunde. Das fünfte ist das Parallelenaxiom, das in der Formulierung von Playfair3 folgendermaßen lautet:
Gegeben seien ein Punkt und eine Gerade. Dann gibt es durch diesen Punkt zu dieser Geraden höchstens eine Parallele.
Dieses Parallelenaxiom hat die Mathematiker anderthalb Jahrtausende beunruhigt. Es sah so anders aus als die anderen vier. Braucht man es wirklich? Oder ergibt es sich aus den anderen? Erst GAUSS2, Bolay2 und Lobaschewski2 konnten zeigen, dass man auch sinnvolle Geometrie treiben kann, wenn man dieses Axiom verneint. Und was zunächst als reine Gedankenspielerei erschien, bekam plötztlich große Bedeutung, als im Gefolge der Relativitätstheorie denkbar wurde, dass dem Kosmos eine solche Geometrie zu eigen ist. (Weil bei Verneinung des Parallelenaxiom die Winkelsumme im Dreieck größer oder kleiner als 180° werden kann, versuchen die Astronomen, durch genaueste Winkelmessungen herauszubekommen, was Sache ist. Leider können sie nicht alle drei Eckpunkte eines astronomischen Dreiecks betreten.)
Bei Euklid sieht das entsprechende Axiom viel rätselhafter aus:
Es gelte: wenn eine Gerade zwei andere Geraden schneidet und wenn die Summe der Innenwinkel auf einer Seite kleiner ist als 180°, dass dann die beiden Geraden sich auf derjenigen Seite schneiden, wo die Summe der Innenwinkel kleiner ist als 180°.
Dass die beiden Formulierungen gleichwertig sind kann man nachweisen. Ich will den Beweis hier nicht vollständig ausarbeiten, sondern nur zeigen wie aus Playfairs Axiom Euklids Axiom folgt, und auch davon nur die wesentlichen Ideen skizzieren.
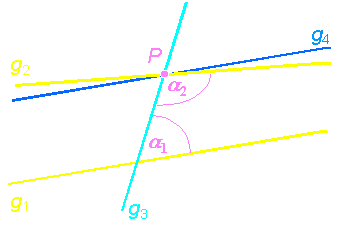
Die Geraden g1 und g2 werden von der Geraden g3 so geschnitten, dass die Summe der Innenwinkel auf der rechten Seite kleiner als 180° ist. Das ist der Wenn-Satz aus EUKLIDs Axiom. Nehmen wir einmal an, der zugehörige Dann-Satz gälte nicht, es gäbe da rechts keinen Schnittpunkt. Dann wären die Geraden parallel. Parallel sind aber auch g1 und g4. Also gäbe es zu g1 zwei verschiedene Parallelen durch P. Das widerspräche PLAYFAIRs Axiom. Also haben wir Unsinn angenommen, als wir sagten, es gebe da rechts keinen Schnittpunkt, und das ist der Beweis, dass es doch einen geben muss (wo immer der liegen mag).
Wenn die beiden Formulierungen gleichwertig sind, warum treibt EUKLID dann solchen Aufwand? Es ist nicht anzunehmen, dass er auf die „einfache” Version nicht auch gekommen wäre. Der Grund muss tiefer liegen, aber darüber können wir nur spekulieren. Womöglich hat ihm der Beweis als solcher nicht gefallen. Offenkundigen Unsinn anzunehmen, zu zeigen dass aus Unsinn Unsinn folgt und damit den Beweis zu führen, das ist wahrlich nicht jedermanns Geschmack. Zumal man dadurch keinerlei Hilfe bekommt, wie man sich denn diesen ominösen Schnittpunkt verschaffen kann. Dann ist es doch ehrlicher, seine Existenz im Axiom zu fordern, als zu solch gewagten Schlüssen Zuflucht zu nehmen.
Der Ausweg, anstatt eines „positiven” Beweises nur nachzuweisen, dass das Gegenteil Unsinn wäre – der sogenannte indirekte Beweis –, setzt voraus, dass zwischen einer Aussage und ihrem Gegenteil kein Platz mehr ist für andere Denkmöglichkeiten, dass jedwedes Drittes ausgeschlossen ist. Dieses tertium non datur – deutsch: es gibt kein Drittes – ist ein sehr hilfreiches logisches Axiom, aber eben nur ein Axiom, und keine ewige Wahrheit. Als Axiom kann man es akzeptieren oder ablehnen, und in jedem dieser beiden Fälle kann man logische Satzgebäude auftürmen. Man kommt eben nur zu verschiedenen Aussagen – ohne das tertium non datur sind allerdings einige liebgewordene Sätze nicht beweisbar, etwa der, dass jede beschränkte unendliche Folge einen Häufungspunkt besitzt.
Resumée
Mathematik ist ein Spiel nach selbstgewählten Regeln. Sind die Regeln einmal festgesetzt, kann das Spiel beginnen. Während des Spiels sind die Regeln verbindlich. Aber nichts hindert uns, für ein neues Spiel neue Regeln aufzustellen. Hauptsache, dass auch in diesem neuen Spiel das Schließen und Beweisen nach allen Regeln der Kunst vor sich geht. Wobei wir immer daran denken sollen, dass Beweise zwar nach Regeln aufzubauen sind, aber sich nicht aus den Regeln von selbst ergeben,
„… dass Beweise sich ebenso wie Kunstwerke nicht auf Befehl schaffen lassen, sondern durch das immer noch unergründliche Wirken der Eingebung entstehen.” (KAPLAN)4
1 Euklid, Elemente, Buch I, Allgemeiner Grundsatz 1 und Postulat (Axiom) 5 - Eine vollständige Wiedergabe von Euklids Elementen findet sich auf der Website der Clark University
2 zitiert nach Spektrum.de SciLogs
3 Informationen über die genannten (und viele andere) Mathematiker findet manauf der Website der School of Mathematics and Statistics, University of St Andrews, Scotland
4 Kaplan, Robert, Die Geschichte der Null, München: Piper, 20042, ISBN 3-492-23918-8, S. 86