 |
 |
 |
 |
 |
Astronomie am Schreibtisch

Die Gleichungen
Mit einigen wenigen physikalischen Formeln lassen sich weitreichende Erkenntnisse über unser Sonnensystem gewinnen. Wir brauchen dazu nur das allgemeine Gravitationsgesetz und die Formel für die Zentralkraft. Mehr nicht.
Fangen wir mit letzterer an. Kein Körper bleibt freiwillig auf einer Kreisbahn. Gradeaus zu fliegen ist sein Bestreben. Dieses Bestreben wird oft als „Flucht aus der Kreisbahn” interpretiert, dass hat uns die Bezeichnung „Zentrifugalkraft” beschert. Für manchen erweckt das den Anschein, als wolle er „nix wie weg”. Aber auch wenn ein Schleuderball beim Herumwirbeln kräftig am Arm zieht, würde er die Kreisbahn nicht radial, sondern tangential verlassen.
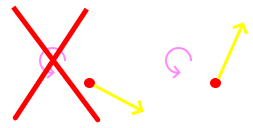
Die Zentralkraft ist diejenige Kraft, die den Körper auf der Kreisbahn hält. Sie hängt ab von der Geschwindigkeit des Körpers. Je schneller er fliegt, desto schwerer ist er zu halten. Das beschert uns den Faktor v
, diesen sogar im Quadrat. Außerdem ist er auf einer engen Bahn viel schwerer zu halten als auf einer weiten. Der Bahnradius spielt ebenfalls eine Rolle, aber eben umgekehrt: kleiner Radius, große Kraft. Deshalb steht der Bahnradius r
im Nenner. Und die Masse des Körpers spielt auch noch mit, wie man sich leicht vorstellen kann. Die Formel für die Zentralkraft lautet:
FZ |
= | m |
· | v2 |
. |
r |
Da der Körper den vollen Kreis mit dem Umfang 2πr
gerade in der Umlaufzeit T
zurücklegt, kann ich die Geschwindigkeit v
gemäß der Beziehung „Geschwindigkeit = Weg durch Zeit” ersetzen durch 2πr
/T
und erhalte damit für die Zentralkraft:
FZ |
= | 4 | π2 |
m |
r2 |
, |
r |
T2 |
|||||
FZ |
= | 4 | π2 |
m |
r |
. |
T2 |
Kommen wir zum Gravitationsgesetz. Zwei Körper ziehen sich gegenseitig an. Das lässt sich mit entsprechend empfindlichen Waagen sogar für Körper von wenigen Kilogramm Masse nachweisen. Dabei kommt es auf beide Massen an. Und auf ihren Abstand. Je größer der Abstand, desto geringer die Anziehung, also auch der wieder im Nenner. Und da zum doppelten Abstand eine auf ein Viertel verringerte Kraft gehört, ist der Abstand r
im Nenner zu quadrieren.
Die Einheit der Kraft ist 1 Newton, aufgedröselt in die Grundeinheiten 1 (Kilogramm mal Meter durch Sekunde hoch zwei). Bei der Zentralkraft passt das genau. Aber bei der Massenanziehung kommt es nicht hin, wenn wir einfach nur die Massen multiplizieren und durch das Quadrat des Abstandes dividieren. Aus diesem Grunde ist noch eine Konstante vonnöten. Diese Konstante hat auch noch einen von 1 abweichenden Zahlenwert. Das kommt daher, dass die Grundeinheiten ohne Rücksicht auf die Massenanziehung festgesetzt sind. Man hatte dabei andere Zusammenhänge im Kopf. Mit dieser Gravitationskonstanten f
erhalten wir das allgemeine Gravitationsgesetz
FG |
= | f |
· | m1 |
· | m2 |
. |
r2 |
Die Gravitationskonstante f
lässt sich mit den genannten empfindlichen Waagen im Labor messen. Sie beträgt
f= 6,67259 ·10-11 N m2 kg-2 .
Der entscheidende Gedanke ist: Für einen Körper, den die Gravitation auf eine Kreisbahn zwingt, liefert die Gravitationskraft gerade die erforderliche Zentralkraft.
FZ =
FG.
Erdmasse
Auf einen Körper der Masse 1 kg wirkt auf der Erdoberfläche die Gravitationskraft 9,807 N. Wir vereinfachen die Verhältnisse dahingehend, dass wir uns die Erdmasse und die 1-kg-Masse jeweils sehr kompakt, sozusagen punktförmig vorstellen und den ganzen Zwischenraum absolut leer. Das ist zwar nicht ganz korrekt, aber für uns im Augenblick genau genug.
Über das Gravitationsgesetz kommen wir zur Gleichung
| 9,807 | kg | m | s-2 | = | f |
· | 1 | kg | · | mE |
. |
R2 |
Darin sind m
E die Erdmasse und R
der Erdradius. Wenn wir uns erinnern, dass die Längeneinheit Meter ursprünglich als der zehnmillionste Teil eines Meridianquadranten festgesetzt war, beträgt also der Erdumfang 40 000 000 m und der Erdradius mithin
R= 40 000 000 m / (2
π) = 6 366 000 m.
mE = 5,966 · 1024 kg,
(Kuchling1: 5,974 · 1024 kg)
Wo wir gerad dabei sind: die mittlere Dichte des Erde ist dann
ρ |
= | mE |
|||
| 4/3 | π |
R3 |
|||
ρ |
= | 5 515 | kg | m-3 | . |
Granit und anderes Steinmaterial hat eine Dichte von ungefähr 3000 kg m-3, ist also deutlich leichter als der errechnete Wert. Erdreich und Wasser fallen noch weniger ins Gewicht. Da werden wohl im Erdinnern erhebliche Mengen von schwererem Material lagern. Wir wissen heute, dass die Erde einen großen Kern aus den schweren Elementen Eisen und Nickel besitzt.
Satelliten, Mond
Wie schnell muss sich ein Körper in der Nähe der Erdoberfläche bewegen, damit er nicht zurück auf die Erde fällt, sondern auf einer Kreisbahn die Erde umrundet? Der Ansatz F
Z = F
G führt auf die Gleichung
mK |
· | v2 |
= | f |
· | mK |
· | mE |
, |
R |
R2 |
||||||||
v2 |
= | f |
· | mE |
. | ||||
R |
Daraus errechnet sich die sogenannte erste kosmische Geschwindigkeit zu
v1 = 7910 m s-1 .
Hervorzuheben ist, dass hierbei die Masse des bewegten Körpers keine Rolle spielt. Mit dieser Geschwindigkeit benötigt der Körper für einen Umlauf um die Erde etwas mehr als 5000 Sekunden, in dieser Größenordnung liegt die Umlaufzeit der erdnahen Satelliten.
Fernsehsatelliten wie Astra kreisen auf einer geostationären Bahn, d. h. sie scheinen über einem Punkt des Äquators stillzustehen, umlaufen aber in Wirklichkeit die Erde in 24 Stunden, genau genommen in einem Sternentag von 86 164 Sekunden. Sie müssen in größerer Höhe kreisen.
| 4 | π2 |
m |
r |
= |
f |
m |
mE |
, |
T2 |
r2 |
|||||||
r3 |
= |
f |
mE |
T2 |
, | |||
| 4 | π2 |
|||||||
r |
= |
4,22 | · | 107 | m | . |
Der gerade aufgetretene Zusammenhang
r3 = const ·
T2
Die dritten Potenzen der Bahnradien– bei Ellipsen:
der großen Halbachsen – verhalten sich wie die Quadrate der Umlaufzeiten.
Genauso können wir mit dem Mond verfahren. Seine Umlaufzeit beträgt 27,322 Tage. Diese Zeitspanne ist kürzer als die Zeit von Neumond bis Neumond – die synodische Umlaufzeit – und wird siderische Umlaufzeit genannt, d.h. Umlaufzeit, bezogen auf den Fixsternhimmel. Die Animation mag den Unterschied verdeutlichen. (Den Unterschied von Sonnentag und Sternentag hat man sich ähnlich vorzustellen.)
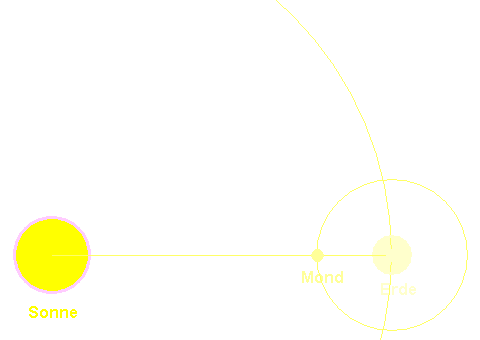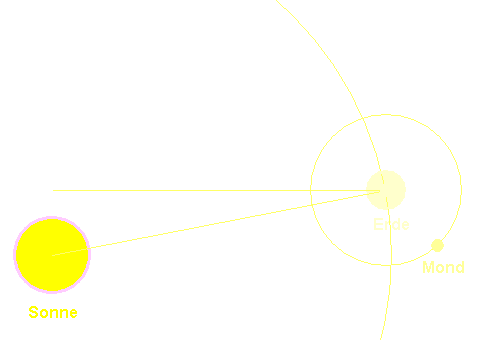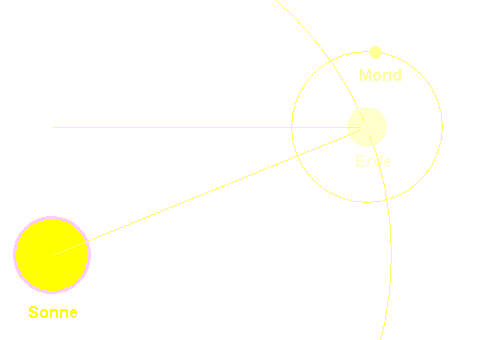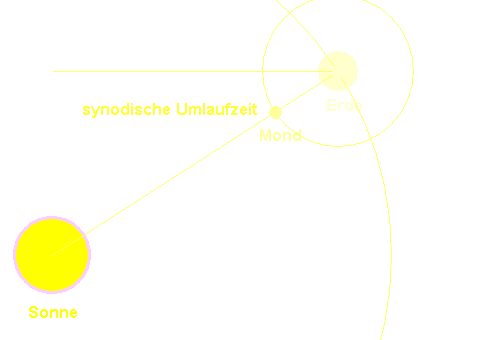
Wir erhalten als Entfernung zwischen den Mittelpunkten von Erde und Mond,
r |
= | 3,832 | · | 108 | m | , |
Sonne
Will man die obige Formel benutzen, braucht man eine der Größen r
oder m
, um die jeweils andere auszurechnen. Über die Enfernung der Erde von der Sonne wissen wir, dass das Licht dazu 8 Minuten braucht, und das bei einer Lichtgeschwindigkeit
v
= 3·108 ms-1.
Das ergibt eine Entfernung von
r |
= | 8 | · | 60 | · | 3 | · | 108 | m | , |
r |
= | 1,44 | · | 1011 | m | , |
Tder Erde dauert 365,25 Sonnentage. Ich stelle die obige Formel um und erhalte
mS |
= |
4 | π2 |
r3 |
, | |
f |
T2 |
|||||
mS |
= |
1,99 | · | 1030 | kg | , |
mS |
= |
332 | 956 | mE |
. |
Planeten
Nachdem wir jetzt auch die Sonnenmasse kennen, können wir mit den Planeten ebenso verfahren, wie vorher mit den Satelliten. Nehmen wir als Beispiel den entferntesten, Neptun. Unsere inzwischen ja bekannte Gleichung liefert den Radius von Neptuns Umlaufbahn
r3 |
= |
f |
mS |
T2 |
, |
| 4 | π2 |
r |
= |
4,495 | · | 1012 | m | . |
r= 4,501 · 1012
Für diese Strecke braucht das Sonnenlicht schon deutlich länger als 4 Stunden!
_____________________1) Alle Vergleichszahlen aus: Kuchling, Horst, Taschenbuch der Physik, Leipzig: Carl Hanser Verlag, 199916, ISBN3-446-21054-7