 |
 |
 |
 |
 |
Unendlichkeit
„Ja”;, grunzelte der Lektro, „prima! Wir suchen uns was aus. Zum Beispiel - ah -: Schwedische Reiter!”;
„Gut. Wieviel?”;
„Ich weiß nicht”;, antwortete der Lektro. „Vielleicht fünfzig.”;
„Ach was, fünfzig. - Fünfzigtausend!”;
„Gut, fünfzigtausend.”;
„Oder hunderttausend!”; rief der Eiskönig. „Hunderttausend bunte schwedische Reiter. Haaaa, man kann sich alles vorstellen, soviel man will! Sagen wir gleich: dreihunderttausend! Oder fünfhunderttausend!”;
„Nein”;, unterbrach ihn der Lektro, „fünfhunderttausend ist zuviel, so viel hat's nie gegeben!”;
„Macht doch nichts, Mensch! Ist doch bunt. Haben Sie Angst? Ich sage: achthunderttausend schwedische Reiter!”;
„Gut”;, gab Lektro nach. Dann rief er: „Eine Million!”;
„Fünfhunderttausend Millionen!”;
„Billionen!”;
„Trillionen”;, rief der Eiskönig.
„Milliarden”;, schrie der Lektro.
„Billiarden!”;
„Trilliarden!”;
„Brillionen!”;
„Oberbrillionen!”;
„Obersuperbrillionen!”;
”;Mir wird's schwindlig”;, sagte der Lektro. „Höher geht's nicht mehr.”;
„Illusionen kommt dann”;, meinte der Eiskönig. „Illusionen sind unerreichbar.”;
„Kann man eine Zahl dazunehmen?”;
„Klar, jede Zahl - bleibt unerreichbar!”1
Unendliche Mengen

Die Vorgehensweise, gleichartige Objekte zusammenzufassen, die in einem engeren Sinne allem Zählen zugrunde liegt, sollte einmal als Mengenlehre für die gesamte Mathematik eine gemeinsame und verlässliche Basis bilden. Es war ja auch zu schön, das in der Grundschule geübte Verfahren, grüne und rote, runde und eckige, große und kleine Spielklötze zu sortieren, zu gruppieren, Schnittmengen und Vereinigungsmengen zu bilden, als Urgrund aller Logik zu begreifen. Solange man mit solchen Klötzchenmengen arbeitet, ist die Sache wirklich wunderbar übersichtlich und eindeutig.
Der erste Schrecken stellt sich ein, wenn plötzlich die leere Menge {} dazutritt. Die Verunsicherung, die uns alle bei der ersten Begegnung mit diesem Monster befallen hat, mag eine Vorstellung davon vermitteln, was für eine intellektuelle Glanzleistung die Einführung der Zahl 0 darstellt.
Wieviel größer ist die Verunsicherung, wenn dann sogar von unendlichen Mengen die Rede ist. Wenn man zum ersten Mal bemerkt, dass das Zählen immer weiter geht, dass man auch bei schwindelnd hohen Zahlen immer noch höher klettern an und in alle Ewigkeit niemals an ein Ende gelangt. Wenn man zu der Einsicht gelangt, dass es unendlich viele Zahlen geben muss.
Abzählbarkeit
Schon stellen sich die nächsten Ungereimtheiten ein. Natürlich gibt es weniger gerade als natürliche Zahlen, es fehlen ja die ungeraden. Andererseits sind es aber auch gleichviele, wie folgende Gegenüberstellung zeigt:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | . | . | . | |||||||||||
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | . | . | . |
Die geraden Zahlen lassen sich eins zu eins – „bijektiv” lautet der Fachausdruck – den natürlichen Zahlen zuordnen. Zu jeder Zahl aus der oberen Zeile gehört eine Zahl aus der unteren Zeile und umgekehrt. Und jede natürliche Zahl kommt in der oberen Zeile irgendwann einmal dran, genauso wie jede gerade Zahl irgendwann in der unteren Zeile drankommt.
Das erscheint widersinnig. Aber gerade dieses Verhalten ist es, was unendliche Mengen auszeichnet, charakterisiert, sie von endlichen Mengen unterscheidbar macht, dass sie bijektiv auf eine echte - d. h. „ärmere” - Teilmenge abgebildet werden können.
Eigenartigerweise kann man auch die Menge der positiven rationalen Zahlen, d. h. die Menge aller Bruchzahlen, bijektiv auf die Menge der natürlichen Zahlen abbilden. Dabei müsste es Brüche eigentlich viel-viel mehr geben, liegen doch allein zwischen null und eins schon unendlich viele. Der elegante Beweis dazu stammt von Georg Cantor und heißt ihm zu Ehren „daserste Cantorsche Diagonalverfahren”. (Aber ja, es gibt noch ein zweites.)
Das funktioniert so: man schreibt die natürlichen Zahlen einmal nebeneinander und einmal untereinander auf und erhält dadurch eine zweidimensionale Tafel nach folgendem Schema.
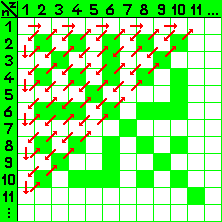
Man fasst die waagerechte Zahlenreihe als die Zähler, die senkrechte Zahlenreihe als die Nenner von Brüchen auf, diese werden in den entsprechenden Feldern notiert. Alle Brüche sind in diesem Schema irgendwann einmal „dran”. Ich lasse jetzt noch alle Brüche weg, die man kürzen kann - im Bild farbig markiert - und folge dann einem schlangenförmigen Gang durch diese Tabelle, wie er durch die roten Pfeile angedeutet ist. Die unterwegs angetroffenen Brüche schreibe ich hintereinander auf und stelle sie den natürlichen Zahlen gegenüber. So ergibt sich eine bijektive Abbildung der natürlichen Zahlen auf die Menge der positiven Brüche.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | . | . | . | |||||||||||
| 1 | 2 | 1 | 1 | 3 | 4 | 3 | 2 | 1 | 1 | 5 | . | . | . | |||||||||||
| 1 | 1 | 2 | 3 | 1 | 1 | 2 | 3 | 4 | 5 | 1 |
Mengen, die bijektiv auf die Menge der natürlichen Zahlen abgebildet werden können, bezeichnet man in der Mathematik als „abzählbar”.
Satz 1: Die Menge N der natürlichen Zahlen ist abzählbar.Satz 2: Die Menge der geraden Zahlen ist abzählbar.Satz 3: Die Menge der positiven Brüche ist abzählbar.
Man könnte auf die Idee kommen, alle unendlichen Mengen seien abzählbar; das aber ist nicht der Fall. Dazu zwei Beispiele.
Erstes Beispiel für Überabzählbarkeit
Zu einer Menge, sagen wir {1, 2, 3, 4} , kann man die Menge aller Teilmengen bilden, in diesem Fall also die Menge
{3,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4} }
Diese sogenannte „Potenzmenge” hat erkennbar mehr Elemente als die Ausgangmenge.In unserem Beispiel hat die Ausgangsmenge 4, die zugehörige Potenzmenge 16 Elemente. Nun ist ja gerade 24 = 16, und tatsächlich gilt der Satz
Satz 4: Ist m die Anzahl der Elemente einer Menge M, so hat die zugehörige Potenzmenge P(M) gerade 2m Elemente.
Der Beweis ist einfach. Nehmen wir zu unserer Beispielmenge noch das Element 5 hinzu, so dass wir von der Menge
ausgehen. Die aufgelisteten 16 Teilmengen bleiben Teilmengen auch für diese neue Menge. Hinzu treten diejenigen Teilmengen, die man aus den vorhandenen durch Hinzunahme des Elementes 5 gewinnt, das sind weitere 16. Durch Hinzunahme eines weiteren Elementes in der Ausgangsmenge hat sich die Potenzmenge verdoppelt, sie hat jetzt 24·2 = 25 Elemente. So geht es immer wieder, und das ist der Beweis. •
Auch von der abzählbaren Menge N kann man die Potenzmenge bilden. Lasst uns versuchsweise annehmen, diese sei ebenfalls abzählbar. Dann könnte man die Teilmengen durchnummerieren und auf diese Weise bijektiv auf die natürlichen Zahlen abbilden.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | . | . | . | |||||||||||
| T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | T11 | . | . | . |
Wir bilden eine weitere Teilmenge T* vermöge folgender Vorschrift: Zu Anfang ist das T* leer. Jetzt schauen wir in T1 nach, ob die 1 darin enthalten ist. Nur wenn das nicht der Fall ist, nehmen wir die 1 in T* auf. Wir schauen in T2 nach, ob die 2 darin enthalten ist. Nur wenn das nicht der Fall ist, nehmen wir die 2 in T* auf. Wir schauen in T3 nach, ob die 3 darin enthalten ist . . . (usw.)
T* ist also gewiss nicht identisch mit T1; denn wenn T1 die 1 nicht enthält, liegt diese aber in T*; wenn T1 die 1 enthält, kommt sie in T* nicht vor, an anderer Stelle kann sie ja nicht hineingeraten sein. Ebenso ist T* nicht identisch mit T2, T3, T4, . . . Kurz, T* kommt in unserer Auflistung überhaupt nicht vor. Die Tabelle ist unvollständig und stellt mithin keine bijektive Abbildung dar. Eine solche kann es gar nicht geben; denn bei jeder Auflistung kann man wie dargelegt die Unvollständigkeit nachweisen. •
Satz 5: P(N) ist überabzählbar.
Zweites Beispiel für Überabzählbarkeit
Die reellen Zahlen enthalten die natürlichen Zahlen, sie enthalten die Bruchzahlen, sie enthalten noch viel mehr, z. B. die nicht aufgehenden Wurzeln, die dritten, vierten, fünften Wurzeln, die Zahl π, die Zahl e, die Logarithmen und - und - und -
Sie alle lassen sich in Form von Dezimalbrüchen schreiben, die Bruchzahlen sogar in Form von abbrechenden oder periodischen Dezimalbrüchen, die andern in Form von nicht-periodischen, nicht-abbrechenden Dezimalbrüchen. Wir beschränken uns auf die reellen Zahlen zwischen 0 und 1. d. h. auf das Intervall (0; 1). Die haben alle eine 0 vor dem Komma, sie sehen so aus:
Die ai sind irgendwelche Ziffern von 0 bis 9. Jetzt bedienen wir uns des zweiten Cantorschen Diagonalverfahrens. Wir nehmen wieder eine bijektive Abbildung an zwischen (0; 1) und N. Wir erhalten folgende Gegenüberstellung:
| 1 | 0, | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | ... |
| 2 | 0, | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b10 | b11 | ... |
| 3 | 0, | c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 | c10 | c11 | ... |
| 4 | 0, | d1 | d2 | d3 | d4 | d5 | d6 | d7 | d8 | d9 | d10 | d11 | ... |
| 5 | 0, | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | e10 | e11 | ... |
| 6 | 0, | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | ... |
| 7 | 0, | g1 | g2 | g3 | g4 | g5 | g6 | g7 | g8 | g9 | g10 | g11 | ... |
| 8 | 0, | h1 | h2 | h3 | h4 | h5 | h6 | h7 | h8 | h9 | h10 | h11 | ... |
| 9 | 0, | i1 | i2 | i3 | i4 | i5 | i6 | i7 | i8 | i9 | i10 | i11 | ... |
| 10 | 0, | j1 | j2 | j3 | j4 | j5 | j6 | j7 | j8 | j9 | j10 | j11 | ... |
| 11 | 0, | k1 | k2 | k3 | k4 | k5 | k6 | k7 | k8 | k9 | k10 | k11 | ... |
| : | . | . | . |
Lauter nicht-abbrechende Dezimalzahlen. Abbrechende Dezimalzahlen denken wir uns durch angehängte Ziffern 0 zu nicht-abbrechenden erweitert. Die indizierten Buchstaben stehen wieder für irgendwelche Ziffern 0 bis 9. Die Bedeutung der hervorgehobenen Stellen wird sich gleich erschließen.
Wir konstruieren uns wieder eine solche Dezimalzahl, die in der Auflistung nicht vorkommt, und zeigen damit die Vergeblichkeit allen Mühens, eine bijektive Abbildung auf N zu finden. Die zu konstruierende Zahl z beginnt natürlich mit ‚null Komma’. Dann schauen wir in der ersten Zeile die erste Ziffer nach dem Komma an, das a1. Steht dort eine 0, so lassen wir z - nach dem Komma - mit 1 beginnen. Steht dort keine 0, so lassen wir das z stattdessen mit 0 beginnen. Jetzt gehen wir zur zweiten Zeile der Auflistung. Hier schauen wir uns die zweite Ziffer b2 an. Steht dort eine 0, so setzen wir z mit 1 fort. Steht dort keine 0, so setzen wir stattdessen das z mit 0 fort usw.
Die solcherart gefundene Zahl z stimmt mit keiner der aufgelisteten Zahlen überein, weil sie sich von jeder an mindestens einer Stelle unterscheidet. z kommt in der Auflistung nicht vor, die Auflistung ist unvollständig. Jede versuchte Auflistung kann so als unvollständig erwiesen werden. Es gibt keine bijektive Abbildung zwischen (0; 1) und N. •
Satz 6: Die reellen Zahlen zwischen 0 und 1 sind überabzählbar.
Ausblick
Kehren wir noch einmal zu unserem ersten Beispiel, der Potenzmenge von N zurück. Diese war „mächtiger” als die Menge N. Das Verfahren, Potenzmengen zu bilden, lässt sich wiederholen, wir können P(P(N)), P(P(P(N))), P(P(P(P(N)))) usw. bilden und auf diese Weise zu immer mächtigeren und schwindelerregenderen Unendlichkeiten aufsteigen, die sich irgendwo im Nebel des Unfassbaren verlieren. Die Frage ist erlaubt: macht das überhaupt noch Sinn?
Die Mathematik hält hierzu eine Theorie der „transfiniten Kardinalzahlen” bereit. Aber gibt es die denn wirklich? - Machen wir uns klar, dass es auch die gewöhnlichen Zahlen nicht in demselben Sinne wirklich gibt wie einen Stein, ein Hund oder ein Auto. Zahlen sind reine Produkte unseres Denkens. Wir hatten nur sehr viel Zeit uns daran zu gewöhnen; deshalb erscheinen sie uns vertraut, vernünftig, praktisch und sinnvoll. Um damit Mathematik treiben zu können, reicht es aus, darüber widerspruchsfrei nachdenken zu können. Und genau das wollen wir auch mit den Unendlichkeiten: widerspruchsfrei darüber nachdenken können. Denn auch sie sind nur Produkte unseres Denkens.
Und was soll das Ganze? Braucht man das irgendwo? Derzeit wohl nicht, um eine Brücke, ein Flugzeug oder einen Computer zu bauen, auch nicht, um Bilanzen zu erstellen oder Geschäftsabläufe zu optimieren. Aber auch die Theorie der komplexen Zahlen wurde nicht aus technischer Notwendigkeit heraus entwickelt, sondern aus dem Gefühl, dass an dieser Stelle noch etwas fehlt, um gewisse mathematische Zusammenhänge zu verstehen. Und sie hat doch nachträglich in der Wechselstromlehre und in der Quantenphysik unmittelbare praktische Bedeutung erlangt. Wenn uns die Theorie der Unendlichkeiten nur hilft, einige schwierige mathematische Sachverhalte besser zu verstehen oder leichter zu begründen, oder wenn sie uns zeigt, wie weit uns reines Denken und logisches Schließen bringen kann, ist das für den Augenblick Rechtfertigung und Sinn genug.
____________________1 Zimnik, Rainer, Geschichten vom Lektro, Berlin: Cecilie Dressler Verlag, 1962, S. 28 ff