 |
 |
 |
 |
 |
Antinomien
(Rückbezüglichkeit 3)
„Der Affe unterscheidet sich vom Menschen nur durch das Fehlen der Sprache. Könnte er nämlich sagen : ‚Ich bin ein Affe’, dann wäre er schon ein Mensch.”1)
Paradoxien
Mit Widersprüchen - scheinbaren oder wirklichen - kann man Menschen ganz schön auf's Glatteis führen. Z. B. mit diesen beiden Sätzen entgegengesetzten Inhalts, die beide wahr sind:
Oder mit diesen beiden, die, obwohl entgegengesetzten Inhalts, beide falsch sind:Dieser Satz weist zweiundvierzig Buchstaben auf 123456 7890 12345 67890123456789 0123456789 012 Dieser Satz weist nicht zweiundvierzig Buchstaben auf 123456 7890 12345 67890 12345678901234 5678901234 567
Dieser Satz hat zweiundvierzig Buchstaben 123456 7890 123 45678901234567 8901234567 Dieser Satz hat keine zweiundvierzig Buchstaben 123456 7890 123 45678 90123456789012 3456789012
Den meisten wird aber sehr schnell klar, dass da tatsächlich gar keine Widersprüche vorliegen. Diese Sätze sprechen ja nicht von derselben Sache. Satz 1 spricht über Satz 1, Satz 2 über Satz 2 usw. Und jeder dieser Sätze hat nun mal eine andere Anzahl von Buchstaben. Das ist also gar keine Antinomie, sondern nur eine verwirrende Spielerei.
„Alle Kreter lügen”
In der Antike galten die Bewohner der Insel Kreta durch die Bank als verlogen. Vermutlich hing das damit zusammen, dass sie den Griechen vorzugsweise als Kaufleute unter die Augen kamen. Und die hatten schon immer eine schlechte Presse, weil sie dazu neigen, die Beschaffenheit ihrer Ware nur im allerbesten Licht darzustellen. (Nicht umsonst war der Götterbote Hermes gleichzeitig der Gott der Kaufleute und Diebe.) So war es ein geflügeltes Wort, dass „alle Kreter lügen”. Man sieht, nationale Vorurteile sind keine Erfindung unserer Zeit.
Das Vergnügen an Spitzfindigkeiten hat schon bald die Frage aufgeworfen, wie das denn nun ist, wenn ein Kreter selber den Satz ausspricht „alle Kreter lügen”. Lügt er dann oder wie oder was? Das hängt sehr davon ab, wie wir diesen Satz lesen. Verstehen wir ihn so, dass Kreter generell einen Hang zur Unwahrheit haben, dann macht er kein Problem. Denn nichts könnte sie dann davon abhalten, auch mal eine ungelogene Äußerung zu tun, zumal wenn es einen geschäftlichen Vorteil verspräche.
Verstehen wir den Satz allerdings so, dass es keinen Kreter gibt, der zu irgendeinem Zeitpunkt die Wahrheit sagt, dann haben wir anscheinend ein echtes Problem. Wirklich? Auch nicht. Jener Kreter behauptet zwar, dass es so sei, aber er kann ja in diesem Moment gelogen haben und die Kreter sind in cumulo doch nicht so schlimm, wie dieser Nestbeschmutzer es darstellt.
Wie aber, wenn wir aus anderer Einsicht zuverlässig wissen, dass alle Kreter überall und immerzu lügen?.Das würde bedeuten, dass kein Kreter jemals eine Wahrheit über die Lippen brächte. Dann kann ein Kreter es gar nicht schaffen, den obigen Satz auszusprechen. Wenn doch, lässt das nur einen Schluss zu: unser Wissen ist doch nicht so zuverlässig, wie wir angenommen haben. Also: wenn ein Kreter sagt „alle Kreter lügen”, dann müssen wir schließen, dass es einen Kreter gibt, der irgendwann einmal die Wahrheit sagt.
Wir haben hier ein sehr schönes Beispiel für einen indirekten Beweis:
Satz: Wenn ein Kreter sagt, dass alle Kreter immerzu lügen, dann gibt es einen Kreter, der irgendwann einmal die Wahrheit sagt.indirekter Beweis: Sei K ein Kreter. K möge sagen, dass alle Kreter immerzu lügen.Annahme: Alle Kreter sagen immerzu und überall die Unwahrheit.1. Fall: K hat recht. Dann hat er selbst einmal nicht die Unwahrheit gesagt. Das widerspricht der Annahme.2. Fall: K hat nicht recht, wenn er behauptet dass alle Kreter immerzu und überall lügen. Sie lügen also nicht immerzu und überall. Auch das widerspricht der Annahme.Wie auch immer, in jedem Fall ist die Annahme zu verwerfen. Ergo: Nicht alle Kreter sagen immerzu und überall die Unwahrheit. Oder anders formuliert: Es gibt einen Kreter, der zu irgendeinem Zeitpunkt (auch einmal) die Wahrheit sagt. •(Anmerkung: das kann K sein oder ein anderer Kreter, darüber sagt unser Beweis nichts.)
Es ist also nichts Widersprüchliches daran zu finden, wenn ein Kreter konstatiert, dass alle Kreter lügen. Es handelt sich hier mitnichten um eine Antinomie, sondern nur um ein Paradoxon - auf den ersten Blick verquer, aber bei genauerer Betrachtung einfach eine unzutreffende Aussage.
Russellsche Antinomie
Von Russell stammt die Antinomie vom Barbier, der alle Männer des Dorfes rasiert, die sich nicht selbst rasieren. Auch hier lässt unsere Umgangssprache wieder verschiedene Deutungen zu. Bezeichnen wir mit Rxy das zweistellige Prädikat „x rasiert y”, mit D die Menge der Männer des Dorfes, so kann die Aussage folgendermaßen präzisiert werden:
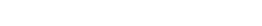
Es gibt einen Mann x, derart dass für alle Männer y gilt: wenn y den y nicht rasiert, rasiert x den y. In dieser Form haben wir überhaupt kein Problem. Wenn x alle Männer rasiert, die sich nicht selbst rasieren, schließt das keinesfalls aus, dass er auch noch den ein oder anderen rasiert, der sich, hin und wieder oder regelmäßig, selbst rasiert, so zum Beispiel auch sich selber.
Nach einer kleinen Veränderung sieht das allerdings ganz anders aus. Ersetzen wir den Pfeil durch einen Doppelpfeil, so erhalten wir
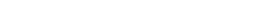
Es gibt einen Mann x, derart dass für alle Männer y gilt: genau dann, wenn y den y nicht rasiert, rasiert x den y. Betrachten wir die Konsequenzen:
Sei x0 ein Mann mit der genannten Eigenschaft,nämlich dass er jeden y rasiert, genau dann wenn dieser sich nicht selbst rasiert.x0 ist selber ein Mann aus dem Dorf,was für alle y gilt, muss deshalb auch für x0 gelten,also gilt: ¬Rx0x0↔Rx0x0 .Das aber ist eine Kontradiktion. •
Wir sehen, die angegebene Aussage führt unweigerlich zu einem Widerspruch. Einen solchen Barbier kann es nicht geben. Wie aber, wenn diese Aussage aus einer wie auch immer gearteten Barbier-Theorie hergeleitet werden könnte? Dann wäre diese Barbier-Theorie widersprüchlich, und so etwas ist das Letzte, was wir bei einer Theorie tolerieren. Denn wo ein Widerspruch ist, da sind auch noch mehr, und in einer Theorie mit Widersprüchen ist auf gar nichts mehr Verlass.
In Wirklichkeit liegt RUSSEL nichts an spitzfindiger Unterhaltung. Er benutzt vielmehr dieses Beispiel als Illustration, um auf ein Problem mit der Mengenlehre hinzuweisen. Dort geht es nicht um Männer, die sich selbst rasieren, sondern um Mengen, die sich selbst als Element enthalten. So etwas ist ja theoretisch immerhin denkbar, wenn es auch bei Mengen konkreter Gegenstände nicht vorkommt.
Das Problem resultiert daraus, dass die Mengenlehre das Zusammenfassen von Objekten zu immer neuen Mengen zulässt, so auch die „Menge aller Mengen”. In dieser Menge aller Mengen gäbe es unter vielen anderen eine „Menge aller derjenigen Mengen, die sich nicht selbst als Element enthalten”. Da haben wir das Pendant zum Barbier, und in der Mengenlehre ein Problem.
Man vermeidet diese Klippe, indem man mit dem Bilden immer neuer Mengen vorsichtig zu Werke geht und insbesondere die Menge aller Mengen genau so sorgfältig vermeidet wie die Division durch null. Wir wissen allerdings nicht, ob das wirklich hilft. Zum Glück sind bislang unter dieser Einschränkung keine neuen Widersprüche entdeckt worden; das gibt zumindest Mut zur Hoffnung.
1Krämer, Wolfgang (Hrsg.), Lukasburger Stilblüten, Heyne Verlag, o. Jz., S. 71